5.4: Asymmetric Cryptography
Essential Questions
- How can two people who have never met before establish secure communication without sharing a secret key first?
- What makes a key pair "asymmetric," and why can one key encrypt what only the other key can decrypt?
- Why do RSA keys need to be much longer than AES keys to provide equivalent security?
- How does public key cryptography enable secure online shopping, email encryption, and digital certificates?
- What are the practical steps to generate key pairs and encrypt files using tools like OpenSSL?
Overview
Imagine trying to send a secret message to someone you've never met, living on the other side of the world. With symmetric cryptography, you'd face an impossible puzzle: how do you share the secret key needed for decryption without an attacker intercepting it? If you email the key, hackers could read your email. If you call with the key, someone might be listening. This fundamental challenge—called the key distribution problem—seemed unsolvable until the 1970s, when researchers discovered an elegant mathematical solution that revolutionized secure communication.
The breakthrough was asymmetric cryptography, also known as public key cryptography. Instead of using one shared secret key, this system uses two mathematically related keys that work as a pair. One key, called the public key, can be freely shared with anyone—posted on websites, printed on business cards, or distributed through email. The other key, called the private key, must be kept absolutely secret. Here's the mathematical magic: information encrypted with one key can only be decrypted with the other key in the pair.
This lesson explores how asymmetric cryptography enables secure communication between strangers, powers the encrypted web browsing you use every day, and forms the foundation of digital certificates that verify website authenticity. You'll learn to generate your own key pairs, understand why asymmetric keys need to be much longer than symmetric keys, and master the practical skills to encrypt and decrypt data using RSA, the most widely used asymmetric algorithm.
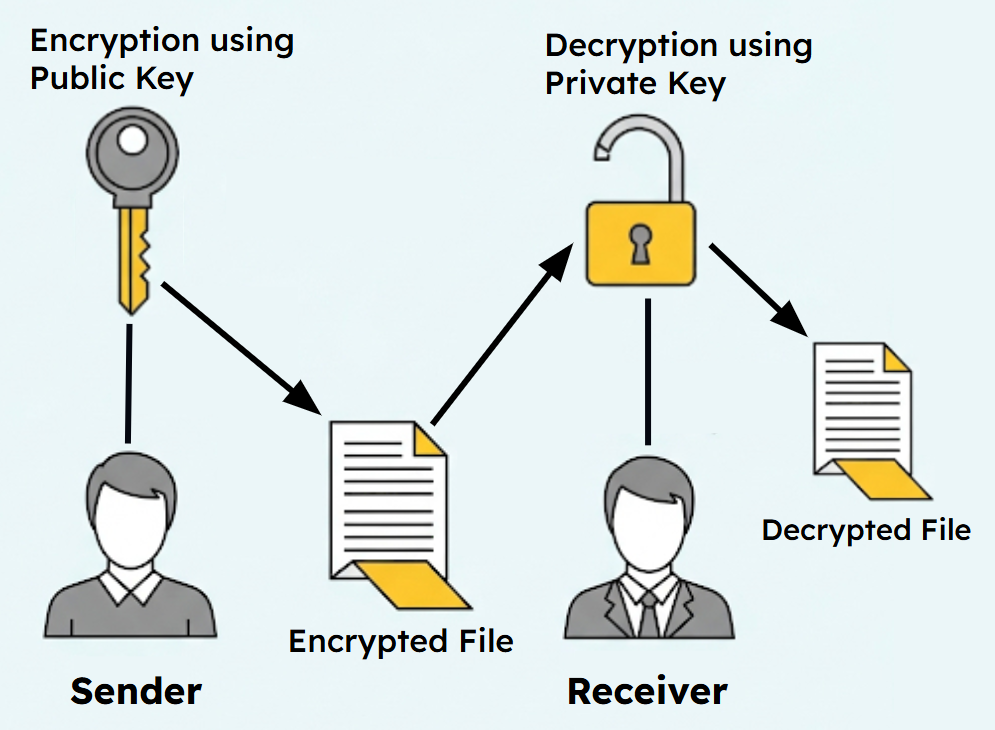
Determine the Appropriate Asymmetric Key to Use When Sending or Receiving Encrypted Data (5.4.A)
Determine the Appropriate Asymmetric Key to Use When Sending or Receiving Encrypted Data (5.4.A)
The revolutionary insight of asymmetric encryption is that it allows secure communication without requiring participants to share a secret key beforehand. This solves one of the most significant challenges in cryptography: how do you establish secure communication with someone you've never met? The answer lies in understanding which key to use for which purpose and how the mathematical relationship between key pairs enables secure messaging.
When you want to participate in asymmetric cryptography, your first step is generating a key pair. These are two binary strings of equal length created simultaneously through a complex mathematical process that ensures they are mathematically related—they are inverses of each other in the context of the encryption algorithm. One key is designated as the public key and the other as the private key. Either key can encrypt information, but only the other key in the pair can decrypt that information.
The security of the entire system rests on a fundamental rule: the private key must remain absolutely secret. If your private key is exposed, shared, stolen, corrupted, or compromised in any way, the entire key pair becomes worthless and must be discarded. You'll need to generate a new key pair and notify everyone who has your old public key.
In contrast, the public key is meant to be distributed as widely as possible. You can post it on your website, include it in your email signature, or upload it to public key servers. The more people who have your public key, the more people can send you encrypted messages. This openness might seem counterintuitive—how can something so public provide security? The answer lies in the mathematical relationship: your public key can only encrypt messages that your private key can decrypt.
Here's how secure communication works in practice: When Alice wants to send a confidential message to Bob, she uses Bob's public key to encrypt the message. Once encrypted with Bob's public key, only Bob's private key can decrypt it—not even Alice can decrypt the message she just encrypted. Bob receives the encrypted message and uses his private key to decrypt it and read Alice's original text.
The key selection process is straightforward but critical: to send a secure message to someone, you encrypt with their public key. To receive and read encrypted messages, you decrypt with your own private key. This creates a secure communication channel that doesn't require Alice and Bob to have met before or to have exchanged any secrets.
Consider a practical scenario: you want to send sensitive financial documents to your accountant. Your accountant generates a key pair and emails you their public key (this email doesn't need to be secure since public keys are meant to be shared). You use their public key to encrypt your financial documents. Even if someone intercepts the encrypted files during email transmission, they can't read the contents because only your accountant's private key can decrypt them.
Interactive Public-Private Key Cryptography
Experience how asymmetric cryptography works with mathematically paired keys. Generate a key pair and discover that only the paired key can successfully decrypt a message.
Key Pair Generation
Encryption Testing
Key Insights:
- • Asymmetric cryptography uses mathematically paired keys
- • What one key encrypts, only the paired key can decrypt
- • Public keys can be shared freely - they're meant to be public
- • Private keys must be kept absolutely secret
- • This solves the key distribution problem of symmetric cryptography
- • Security depends on the mathematical relationship, not key secrecy (for public keys)
Why the Length of a Key Impacts the Security of Encrypted Data (5.4.B)
Why the Length of a Key Impacts the Security of Encrypted Data (5.4.B)
The relationship between key length and security in asymmetric cryptography follows the same fundamental principle as symmetric cryptography, but with dramatically different practical requirements. Longer keys create exponentially larger keyspaces, making brute-force attacks exponentially more difficult. However, asymmetric algorithms require much longer keys than symmetric algorithms to achieve equivalent security levels.
For any binary key of n bits, the keyspace contains 2^n possible keys. An attacker attempting to break the encryption through brute force would need to try, on average, 2^(n-1) keys before finding the correct one. This exponential relationship means that adding just one bit to the key length doubles the work required for an attacker. Adding ten bits increases the work by a factor of 1,024.
However, the security comparison between different algorithms isn't straightforward. A 256-bit AES key provides vastly different security than a 256-bit RSA key. This disparity exists because AES and RSA rely on different mathematical problems. AES security depends on the difficulty of distinguishing the cipher output from random data, while RSA security depends on the difficulty of factoring large numbers into their prime components.
Current recommendations illustrate this difference clearly: A 128-bit AES key provides strong security for most applications, but an RSA key needs to be at least 2048 bits to provide comparable security. For high-security applications, AES-256 (256-bit keys) corresponds to RSA keys of 4096 bits or longer. This means RSA keys are typically 8 to 16 times longer than AES keys for equivalent security.
The practical implications are significant. Longer keys require more computational time and resources for both encryption and decryption operations. A 4096-bit RSA operation takes considerably longer than a 2048-bit RSA operation, which in turn takes much longer than an AES operation with equivalent security. This performance difference is one reason why most secure communication systems use hybrid approaches: asymmetric cryptography to securely exchange symmetric keys, then symmetric cryptography for the bulk data encryption.
Computational processing power continues to improve, which means that keys considered secure today may become vulnerable in the future. Key-length recommendations are periodically updated to account for increased processing power and improvements in attack algorithms. What required a 1024-bit RSA key twenty years ago now requires at least 2048 bits, and many organizations are moving to 4096-bit keys for long-term security.
Cryptographic Algorithm Security Comparison
Compare the security levels and performance characteristics of different cryptographic algorithms. Understand why RSA requires much longer keys than AES to provide equivalent security protection.
AES (Symmetric)
Security Analysis
RSA (Asymmetric)
Security Analysis
Equivalent Security Levels
Your Selected Configuration
Security Comparison
Your AES-128 provides Good security, equivalent to RSA-3072or ECC-256. Your RSA-2048 provides Acceptable security.
Security Equivalency Reference
| Security Level | AES | RSA | ECC | Expected Lifetime |
|---|---|---|---|---|
| Deprecated | 80 bits | 1,024 bits | 160 bits | 1-5 years |
| Acceptable | 112 bits | 2,048 bits | 224 bits | 5-10 years |
| Good | 128 bits | 3,072 bits | 256 bits | 10-20 years |
| Strong | 192 bits | 7,680 bits | 384 bits | 20-30 years |
| Very Strong | 256 bits | 15,360 bits | 512 bits | 30+ years |
Key Insights:
- • RSA requires 8-16x longer keys than AES for equivalent security
- • Security recommendations evolve as computing power increases
- • Performance decreases significantly with longer asymmetric keys
- • ECC provides better security-to-performance ratio than RSA
- • Hybrid systems combine the best of symmetric and asymmetric cryptography
- • Future-proofing requires considering quantum computing threats
Apply Asymmetric Encryption Algorithms to Encrypt and Decrypt Data (5.4.C)
Apply Asymmetric Encryption Algorithms to Encrypt and Decrypt Data (5.4.C)
The most widely used asymmetric encryption algorithm is RSA, named after its inventors Rivest, Shamir, and Adleman. RSA forms the backbone of secure internet communications, digital certificates, and many authentication systems. Understanding how to generate keys and encrypt data with RSA gives you practical skills for implementing secure communication systems.
Like symmetric encryption, asymmetric encryption can be performed using command-line tools, specialized software, or web-based interfaces. OpenSSL remains the most versatile and widely available tool for asymmetric cryptography, providing comprehensive support for RSA key generation, encryption, and decryption.
The first step in any asymmetric cryptography implementation is generating a key pair. With OpenSSL, generating a 2048-bit RSA key pair requires this command:
openssl genrsa -out rsa.pem 2048
This command creates a file called rsa.pem containing both the private and public keys in a single file formatted according to the Privacy-Enhanced Mail (PEM) standard. Since public keys need to be shared while private keys must remain secret, you typically extract the public key into a separate file:
openssl rsa -pubout -in rsa.pem -outform PEM -out public.pem
Encryption with RSA follows the same principle as symmetric encryption but uses public keys instead of passwords. To encrypt a file called test using your RSA public key:
openssl pkeyutl -encrypt -pubin -inkey public.pem -in test -out test.enc
Decryption reverses the process using the corresponding private key:
openssl pkeyutl -decrypt -inkey rsa.pem -in test.enc -out test
Only the holder of the private key can decrypt the file, even though anyone could have encrypted it using the publicly available public key.
Here's a practical scenario that demonstrates the complete workflow: Suppose you're a journalist who needs to receive sensitive documents from sources. You generate an RSA key pair and publish your public key on your website. Sources can download your public key and use it to encrypt documents before sending them to you. Even if the encrypted files are intercepted during transmission, only you can decrypt them with your private key.
# Generate your key pair
openssl genrsa -out journalist.pem 2048
openssl rsa -pubout -in journalist.pem -outform PEM -out journalist-public.pem
# A source encrypts a document for you
openssl pkeyutl -encrypt -pubin -inkey journalist-public.pem -in confidential-doc.txt -out confidential-doc.enc
# You decrypt the document
openssl pkeyutl -decrypt -inkey journalist.pem -in confidential-doc.enc -out confidential-doc.txt
This workflow enables secure communication without requiring any prior secret sharing between you and your sources. Each source independently downloads your public key and encrypts their documents. You use your single private key to decrypt documents from all sources.
Important limitations of RSA encryption affect practical implementations. RSA can only encrypt data smaller than the key size minus padding overhead. A 2048-bit RSA key can encrypt at most about 245 bytes of data directly. For larger files, you typically use hybrid encryption: generate a random AES key, encrypt the file with AES, then encrypt the AES key with RSA. The recipient decrypts the AES key with their RSA private key, then uses that AES key to decrypt the file.
Interactive File Encryption Demo
Experience the complete asymmetric encryption workflow: hybrid encryption using RSA for key exchange and AES for file encryption, plus digital signatures for authenticity.
Encryption Setup
Encryption Process
Key Learning Points:
- • Real-world encryption uses hybrid systems (RSA + AES)
- • Private keys must be kept secret for decryption to work
- • Digital signatures provide authenticity and integrity
- • Key fingerprints help verify you're using the right keys
- • Encryption process has multiple steps, each serving a purpose
- • Wrong keys result in immediate decryption failure
Real-World Applications
Consider how asymmetric cryptography enables secure online shopping. When you visit an e-commerce website, your browser downloads the site's public key (embedded in their SSL certificate). Your browser generates a random symmetric key, encrypts it with the website's public key, and sends it to the server. Only the website can decrypt this symmetric key with their private key. Once both parties have the same symmetric key, they use it for fast symmetric encryption of all subsequent communication. This hybrid approach leverages asymmetric cryptography's key distribution strengths and symmetric cryptography's performance advantages.
Further Reading & Resources
- RSA Laboratories: What is Public-Key Cryptography?
- NIST Special Publication 800-57: Recommendation for Key Management
- OpenSSL Documentation: Public Key Algorithms
- Understanding Cryptography by Paar and Pelzl
- Elliptic Curve Cryptography: A Gentle Introduction